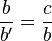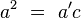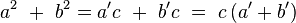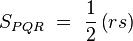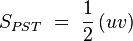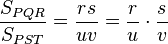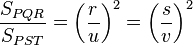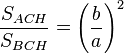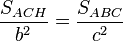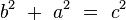viernes, 21 de noviembre de 2014
RELACIONES METRICAS
Las Relaciones Metricas en el Triangulo Rectangulo son teoremas o propiedades, que son validas exclusivamente en el triangulo rectangulo y se aplican sobre las dimensiones de los catetos, hipotenusa, la altura relativa a la hipotenusa y los segmentos determinados sobre esta como proyecciones de los catetos de triangulo.

Dado el triangulo rectangulo ABC, con su angulo recto en C, donde:
c es la hipotenusa
b la altura relativa a la hipotenusa
p y q los segmentos determinados a la hipotenusa
TEOREMAS
Teorema de Pitagoras:
Filosofo y matematico Griego. 582 a.c.-507a.c. Este teorema lleva este nombre porque fue descubierto en la escuela pitagorica. Anteriormente, en Mesopotamia y en el Antiguo Egipto se conocia temas de valores que correspondian con los lados de un triangulo rectangulo, y se utilizaban para resolver problemas con dichos triangulos. La piramide de Kefren fue construida basandose en el triguangulo sagrado egipcio, de proporciones 3-4-5.
Teorema de Euclides:
Matematico y geometra griego, 300 a.c.- 265 a.c. Se desprenden tres relaciones. Estas relaciones se aplican sobre las dimensiones de los catetos, la hipotenusa, la altura relativa a la hipotenusa y los segmentos determinados sobre esta como proyecciones de los catetos
PROPIEDADES
TEOREMA FUNDAMENTAL:
Establecemos la proporción entre sus lados correspondientes:

En cualquier triángulo rectángulo, el producto de las medidas de sus catetos es igual al producto de la medida de la hipotenusa por la medida de la altura relativa a la hipotenusa.
Teorema referido a los catetos:
- En los triángulos rectángulos semejantes CAB y AHB , analizamos la proporción:
- En los triángulos rectángulos semejantes CAB y AHC, analizamos la proporción:
En cualquier triángulo rectángulo , el cuadrado de la medida de un cateto es igual al producto de la medida de la hipotenusa por la medida de la proyección ortogonal de ese cateto sobre la hipotenusa.

- BH es la proyección ortogonal del cateto AB sobre la hipotenusa. Su medida es m.
- HC es la proyección ortogonal del cateto AC sobre la hipotenusa. Su medida es n.
Teorema referido a la altura:
Los triángulos rectángulos AHB y AHC son semejantes :
- Analizamos la proporción :

En cualquier triángulo rectángulo, el cuadrado de la medida de la altura relativa a la hipotenusa es igual al producto de las medidas de las proyecciones ortogonales de los catetos sobre la hipotenusa.


Teorema de Pitágoras:
Observa el triángulo rectángulo CAB:

- Por el Teorema referido a los catetos:
- Sumamos miembro a miembro:

Factorizamos:

En cualquier triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la medida de la hipotenusa.
SEMEJANZA DE TRIANGULOS
Semejanza de triángulos

Los lados a y a', b y b', c y c' se llaman lados homólogos.
Son ángulos homólogos:

Dos triángulos son semejantes cuando tienen sus ángulos homólogos iguales y sus lados homólogos proporcionales.


La razón de la proporción entre los lados de los triángulos se llama razón de semejanza.
La razón de los perímetros de los triángulos semejantes es igual a su razón de semejanza.

La razón de las áreas de los triángulos semejantes es igual al cuadrado de su razón de semejanza.

LEMA DE THALES
Lema: Sean A1, A2, B1, B2 cuatro puntos en el plano afín con A1 distinto de B1. Entonces son equivalentes:
(a) Las rectas A1B1 y A2B2 son paralelas o A2=B2.
(b) El vector A1A2+B2B1 es un múltiplo escalar de A1B1.

Demostración: Cualquiera de las condiciones de (a) implica que existe un escalar h tal que A2B2=h·A1B1; es decir, A2A1+A1B2=h·A1B1; de donde A2A1+B1A1+A1B2=h·A1B1+B1A1, y por tanto, A2A1+B1B2=(h-1)·A1B1.
Recíprocamente, si existe un escalar h tal que A2A1+B1B2=h·A1B1, entonces A2B2=(h+1)·A1B1; si h+1=0 entonces A2=B2 y en otro caso A1B1 y A2B2 son paralelas.
Teorema: En un plano afín, sean ri (i=1,2,3) rectas paralelas distintas dos a dos, y sean s,t rectas no paralelas a las anteriores. Sean Si y Ti los puntos de corte de ri con s y t, respectivamente. Entonces el segmento S1S2 es a S1S3 como T1T2 es a T1T3.

Demostración: Por las condiciones del problema, se tiene a lo sumo una igualdad Si=Ti para un solo i, y podemos asumir que Si es distinto de Ti para i=2 pues en otro caso intercambiamos los papeles de ri y r2. Los vectores S1S2 y S1S3 son no nulos y están en s, luego existe un escalar a tal que S1S3=a·S1S2. Sea T0=T1+a·T1T2, es decir se tiene T1T0=a·T1T2. Como r1 (o sea S1T1) es paralela a r2 (o sea S2T2), el lema nos da un escalar h tal que S1S2+T2T1=h·S1T1. Entonces se tiene S1S3+T0T1=S1S3+a·T2T1=h·S1T1, y de nuevo el lema nos dice que o bien S1T1 y S3T0 son paralelas o bien S3=T0. La primera opción implica que S3T0 es r3 (la única paralelas a r1 que pasa por S3) y por lo tanto T0=T3 (ambos son la intersección de r3 con t). La segunda también implica que T0=T3, pues de lo contrario t sería T0T3, o sea S3T3, o sea r3, contra la hipótesis de que t no es paralela a las ri. Tenemos así S1S3=a·S1S2 y T1T3=a·T1T2, lo que nos da el resultado.
TRIANGULOS NOTABLES
Triángulos Notables
Son aquellos triángulos que a partir de la razón de dos de sus lados se pueden calcular su tercer lado y la medida de sus ángulos internos. Sólo existen dos triángulos rectángulos notables de medidas exactas y son aquellos que se deducen del triángulo equilátero y del cuadrado, estos son los de 30°, 60° y de 45°.

Triángulo Notable de 45º
Triángulo Notable de 30º y 60º
TEOREMA DE PITAGORAS
Teorema de Pitágoras
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
|
Si un triángulo rectángulo tiene catetos de longitudes  y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:
 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:(1)
Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.
- De la semejanza entre ABC y AHC:
y dos triángulos son semejantes si hay dos o más ángulos congruentes.
- De la semejanza entre ABC y BHC:
Los resultados obtenidos son el teorema del cateto. Sumando:
Pero 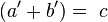 , por lo que finalmente resulta:
, por lo que finalmente resulta:
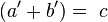 , por lo que finalmente resulta:
, por lo que finalmente resulta:
Pitágoras también pudo haber demostrado el teorema basándose en la relación entre las superficies de figuras semejantes.
Los triángulos PQR y PST son semejantes, de manera que:
siendo r la razón de semejanza entre dichos triángulos. Si ahora buscamos la relación entre sus superficies:
obtenemos después de simplificar que:
pero siendo  la razón de semejanza, está claro que:
la razón de semejanza, está claro que:
 la razón de semejanza, está claro que:
la razón de semejanza, está claro que:
Es decir, "la relación entre las superficies de dos figuras semejantes es igual al cuadrado de la razón de semejanza".
Aplicando ese principio a los triángulos rectángulos semejantes ACH y BCH tenemos que:
que de acuerdo con las propiedades de las proporciones da:
 (I)
(I)
y por la semejanza entre los triángulos ACH y ABC resulta que:
pero según (I) 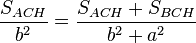 , así que:
, así que:
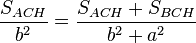 , así que:
, así que:
y por lo tanto:
quedando demostrado el teorema de Pitágoras.
Es asimismo posible que Pitágoras hubiera obtenido una demostración gráfica del teorema.
Partiendo de la configuración inicial, con el triángulo rectángulo de lados a, b, c, y los cuadrados correspondientes a catetos e hipotenusa –izquierda-, se construyen dos cuadrados diferentes:
- Uno de ellos –centro- está formado por los cuadrados de los catetos, más cuatro triángulos rectángulos iguales al triángulo inicial.
- El otro cuadrado –derecha- lo conforman los mismos cuatro triángulos, y el cuadrado de la hipotenusa.
Si a cada uno de estos cuadrados les quitamos los triángulos, evidentemente el área del cuadrado gris ( ) equivale a la de los cuadrados amarillo y azul (
) equivale a la de los cuadrados amarillo y azul ( ), habiéndose demostrado el teorema de Pitágoras.
), habiéndose demostrado el teorema de Pitágoras.
 ) equivale a la de los cuadrados amarillo y azul (
) equivale a la de los cuadrados amarillo y azul ( ), habiéndose demostrado el teorema de Pitágoras.
), habiéndose demostrado el teorema de Pitágoras.
De la ecuación (1) se deducen fácilmente 3 corolarios de aplicación práctica:
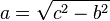 |  | 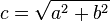 |
Suscribirse a:
Comentarios (Atom)